Ensemble Forecasting
Lifesight Adaptive Forecasting Framework
Motivation
For marketers and data scientists at the helm of measurement platforms (e.g. Lifesight), the ability to predict the impact of marketing spend on business KPIs is not an academic exercise; rather, it is a critical function with profound financial implications. Poor forecasts mean misallocated budgets, wasted ad spend, and missed revenue targets.
Companies that master this are confidently able to optimize their marketing mix, forecast growth, and align marketing efforts with financial goals. Forecasting allows your company to be proactive instead of reactive.
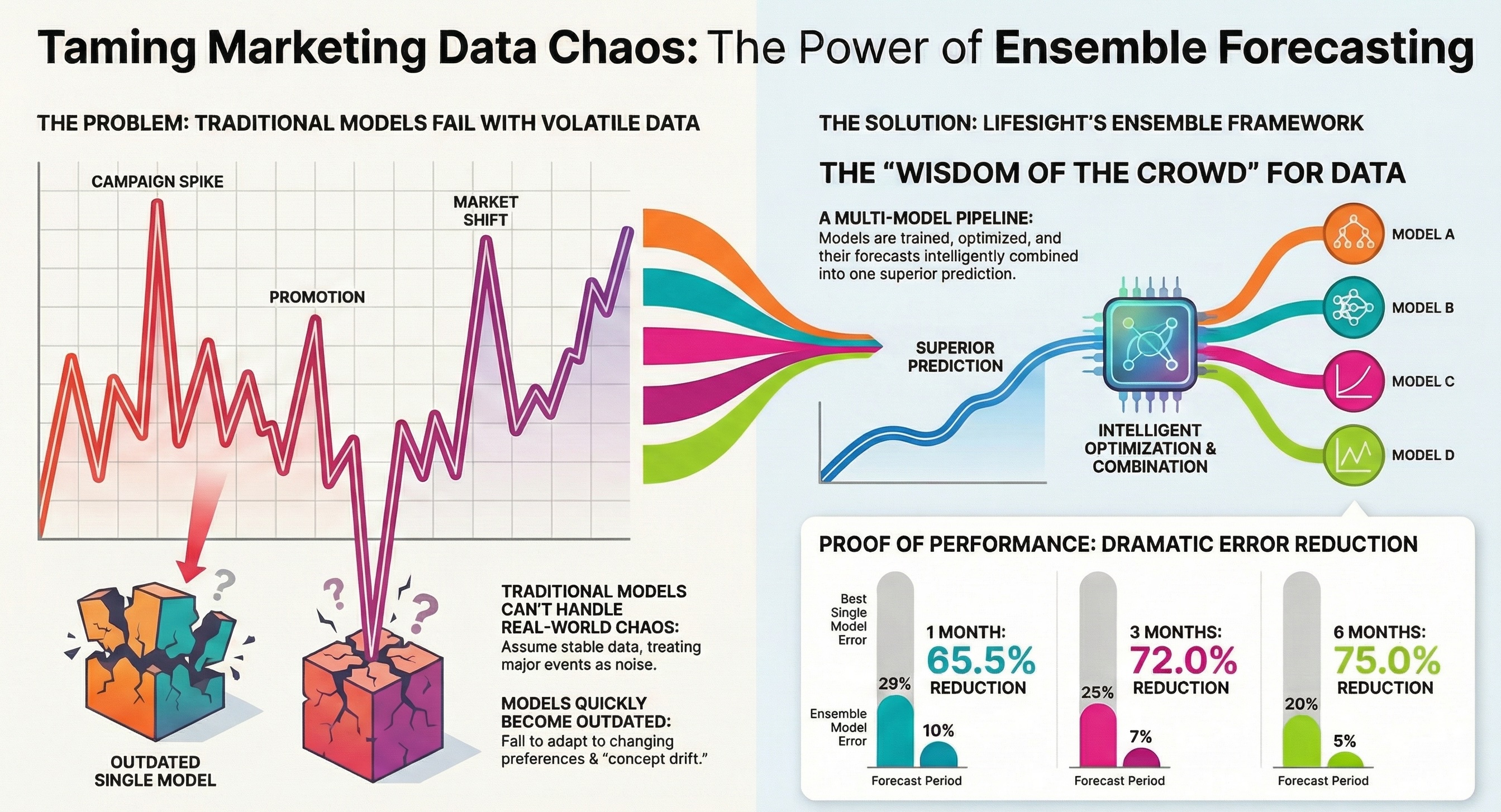
Studies report that traditional approaches—such as ARIMA and exponential smoothing—are hampered by strict assumptions of linearity and stationarity, which fail to capture the complex, non‐stationary patterns of marketing data. Von Krogh et al. (2023) note that while machine learning models offer flexibility, they are nevertheless constrained by issues of data access, bias, and cost.
In contrast, Lifesight Adaptive Forecasting Framework ensembles various algorithms— including supervised, and Bayesian techniques—to reduce individual model weaknesses by leveraging the “wisdom of the crowd.” The reviewed studies conceptually support this approach: ensemble techniques may better account for non-stationarity and dynamic volatility, and they suggest that integrating models with complementary strengths can yield more robust forecasts.
Limitations of Standalone Forecasting Models
Marketing data is heavily confounded by exogenous variables. These interventions like promotions, campaigns, etc.—create spikes and non-stationarities within data distribution.
- Structural Assumptions and Non-Stationarity Classical time series models (ARIMA, exponential smoothing etc) operate under assumptions of stationarity and linearity that are systematically violated in marketing contexts. These methods treat structural breaks like competitor product launches, viral content propagation, algorithmic platform changes etc as statistical noise rather than regime-defining events. This results in forecasts that fail to capture persistent baseline shifts, conflating transient spikes with sustained trend changes.
- Data Hunger and Spurious Pattern Learning DNN (Deep Neural Networks) like LSTM/RNN in concept can model any function with proper depth and layers along with other HyperParameters. However, they require large training datasets (more than few thousands observations) to learn temporal patterns and avoid overfitting. We at Lifesight have constrained 2 years of Marketing data which didn’t provide good performance with DNN even with Optimization.
- Domain expertise for Feature Generation Gradient boosted models require features like Lag features, Rolling statistics, Interaction terms etc for better performance. These features are unique to each data distribution and come with Domain expertise. MMM Platforms like Lifesight, generally don’t have visibility into each domain.
- Model Instability and Concept Drift Marketing Data is inherently non-stationary due to constant change in customer preferences, new launches and ad platform changes. A single model may be able to capture historical data distribution but might fail to understand future perturbations and drift over time.
At Lifesight, we understand that forecasting models cannot be treated as static artifacts; they must be architected as living systems, complete with automated pipelines for performance monitoring, drift detection, and regular retraining to ensure they remain relevant and accurate.
Introduction to Ensemble Forecasting
Ensemble forecasting is a powerful approach that combines multiple models or data sources to improve prediction accuracy and quantify uncertainty, especially in complex, nonlinear systems like marketing, weather and finance etc. This method can include a wide range of techniques, from traditional statistical combinations to advanced machine learning and deep learning models.
Methodology
- Model Combinations
Ensemble forecasting typically merges outputs from diverse models (supervised, deep learning, Bayesian) using simple averages, weighted averages, Bayesian model averaging [1] or optimization algorithms [2] to lower predictive vs actual difference. - Selective Ensembles
Recent advances include dynamic weighting (adapting to changing data patterns) and selective ensembles that choose the best subset of models for each forecast [1, 2]. - The central premise of ensemble forecasting—the "wisdom of the crowd"—relies on the base models being both accurate and diverse (i.e. their errors are uncorrelated).
Algorithms Explored
- Sarimax(Seasonal AutoRegressive Integrated Moving Average with exogenous regressors) is a classical statistical model adept at capturing strong seasonal and autoregressive components [7]. While effective for stationary or near-stationary data, its performance can degrade when faced with abrupt structural changes or complex non-linearities, making it a stable but often rigid baseline model in an ensemble.
- Prophet is a decomposable time series model from Facebook, engineered for scalability and interpretability [5]. It excels at capturing multi-period seasonality and custom holiday effects and is notably robust to missing data and outliers. Its ability to flexibly model non-linear trends makes it a strong candidate for ensembles, often capturing patterns that linear models like SARIMA miss
- Neural Prophet extends the Prophet framework by incorporating neural network components (specifically, an AR-Net) to model time-series autocorrelation and lagged covariates [6]. This allows it to capture more complex non-linearities and interactions, serving as a powerful hybrid model within a diverse ensemble.
- CatBoost is a Gradient Boosting on Decision Trees (GBDT) algorithm, distinguished by its sophisticated internal handling of categorical features [8]. In forecasting, it is frequently leveraged as a powerful non-linear and non-parametric model, demonstrating robust accuracy, especially when large feature sets (e.g. lagged variables, exogenous regressors) are available.
- Bayesian Time Series models offer a probabilistic approach to time-series decomposition. Their primary value in an ensemble context lies in their superior uncertainty quantification (providing full credible intervals) and their ability to adapt to dynamic, non-stationary environments.
This list exemplifies the diverse modeling paradigms we leveraged: from classical statistical methods to modern machine learning and hybrid neural models.
Our final ensemble architecture is not limited to these examples but is the result of a rigorous selection process across a wide stable of algorithms.
Optimization Techniques
- Grid Search systematically explores all possible combinations of hyperparameters. While thorough, it is computationally expensive and inefficient for large parameter spaces.
- Random Search samples hyperparameter combinations randomly. It is more efficient than grid search, especially when only a few hyperparameters significantly impact performance.
- Bayesian Optimization models the performance surface and selects hyperparameters based on probabilistic improvement, leading to faster convergence and more stable results. Bayesian optimization is often more effective and stable than grid or random search, particularly for complex models like CatBoost and XGBoost [10].
Our implementation of these ensemble methods involves a strategic approach to hyperparameter optimization (HPO) for e.g. A key challenge arises with models like SARIMAX when applied to granular (daily) data, where traditional HPO methods like Grid Search or Random Search become computationally infeasible. In this context, Bayesian Optimization presents a highly efficient alternative, consistently delivering comparable predictive performance while substantially mitigating the computational burden.
Ensemble Architecture
This architecture begins with Input Data (with extra features) being fed into multiple distinct Base Models (Model 1 to Model N). Each base model undergoes its own Training & Optimization phase, where its specific hyperparameters are tuned to best capture particular aspects of the data. This leads to individual Forecasts (Forecast 1 to Forecast N) from each model.
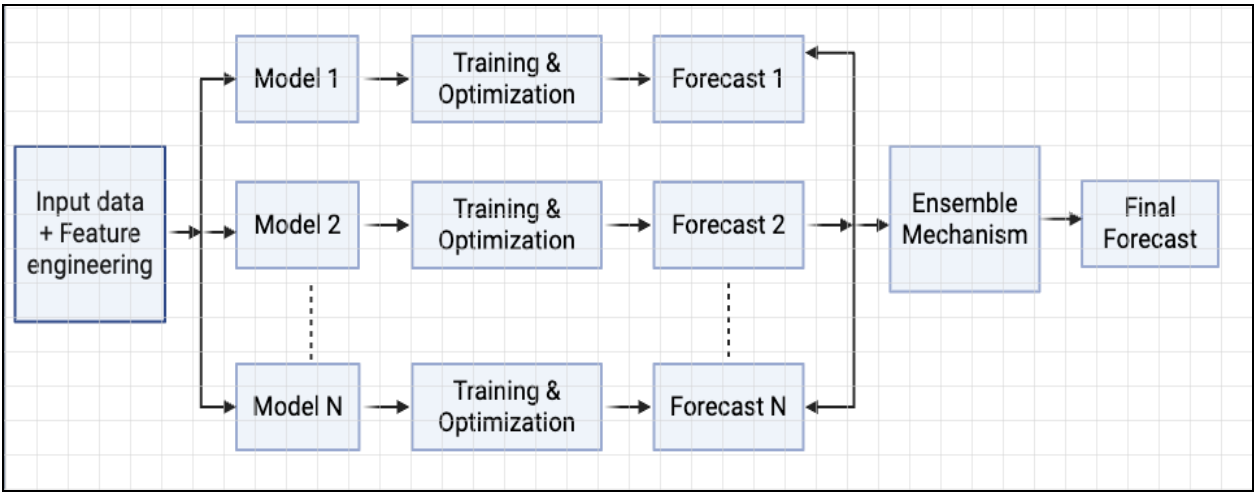
Note: Feature Engineering is specific to each Model.
The power of the ensemble lies in the Ensemble Mechanism, which intelligently combines these diverse individual forecasts. This mechanism is responsible for aggregating the "wisdom of the crowd" by weighting, blending, or meta-learning from the base model outputs. The ultimate goal is to produce a Final Forecast that not only benefits from the varied strengths of each base model but also provides enhanced accuracy and robustness compared to any single model used in isolation.
Ensemble Combination Strategies
Over the years, various ensemble techniques have been developed and studied. Few of the widely used are:
- Simple Average
This foundational method assigns an equal weight (1/N) to all N base models, with the final forecast being the arithmetic mean. As noted by Clemen (1989) and others, this method is "unreasonably effective" and often outperforms more complex weighting schemes [11]. This phenomenon, known as the "forecast combination puzzle," is often attributed to the robustness of the simple average. - Weighted average This approach assigns a unique, static weight to each base model, with the final forecast being the weighted sum. The core challenge lies in determining the optimal weights. Common strategies include: Variance-based, Regression based, Bayesian model average.
- Stacking Stacking treats combining forecasts as a two-level learning problem. Output from the base model is fed as input into a new model, called a "meta-model", to learn the best way to combine the base level forecasts.
Hyperparameter Optimization Strategy
To ensure each base model was operating at peak performance before being integrated into the ensemble, we defined a comprehensive hyperparameter space for each. The optimization of these parameters is crucial, as a poorly tuned model can degrade the entire ensemble. As discussed previously, we leveraged various HPO techniques, including Bayesian Optimization, to efficiently navigate these complex search spaces.
The key hyperparameters tuned for our primary model classes included (below list shared as reference only):
- SARIMAX: The auto-regressive and moving average orders for both non-seasonal (p, d, q) and seasonal (P, D, Q) components. Additionally, the number of Fourier terms used to model complex, multi-period seasonality was a critical parameter.
- Prophet: Optimization focused on the changepoint_prior_scale (to control trend flexibility), seasonality_prior_scale, and the number of fourier_order terms for the seasonality_period.
- CatBoost: As a GBDT model, the search space included the learning_rate, tree depth, l2_leaf_reg for regularization, and the total number of iterations.
- Bayesian Structural Time Series (BSTS): For our Bayesian models, optimization involved selecting the components to include in the model state, such as the stochasticity of the local level like slope, trend, and seasonal components.
Data and Result
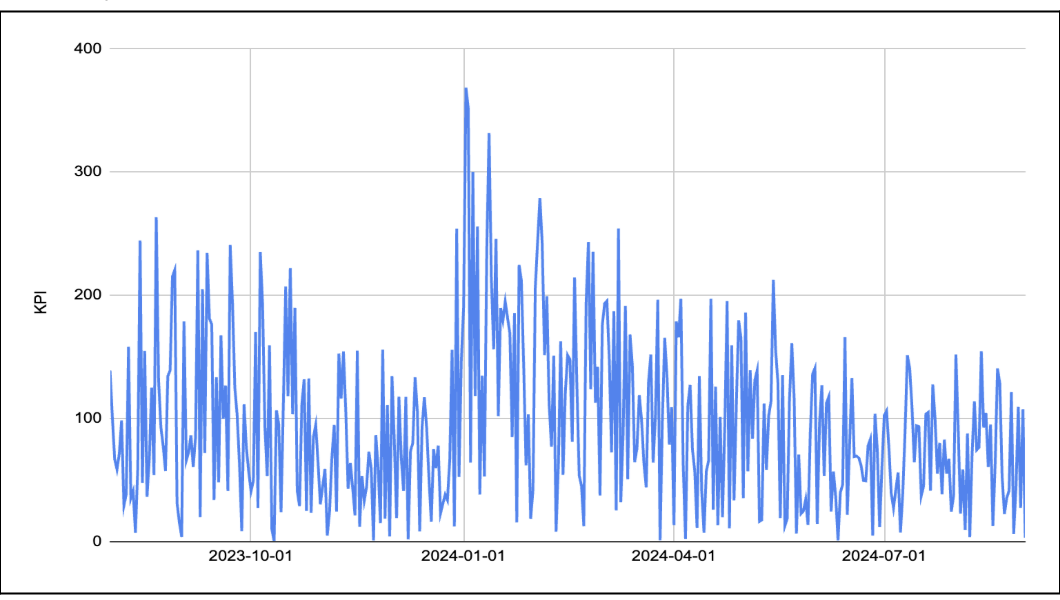
As we already discussed, Marketing data is mostly full of volatility, frequent and significant spikes, indicative of campaigns, promotions, or external market influences. They also possess complex, multi-period seasonality and occasional outlier events. We are demonstrating a few real world examples [modification done to preserve confidentiality].
Company XYZ : Revenue trend over time:
Company PQR: Order trend over time:
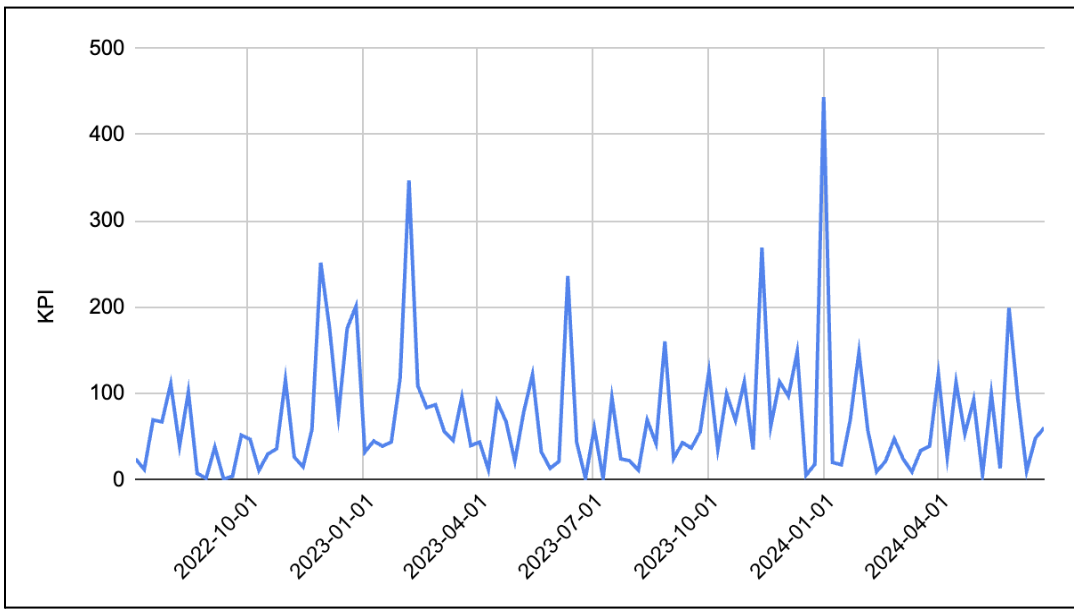
Our experiment confirms that an Ensemble Forecasting methodology is a highly effective solution for the inherent volatility and complexity of marketing data.
To quantify this performance lift, we went beyond standard backtesting and performed a True out-of-time (OOT) validation. The ensemble's forecasts were generated and model combinations selected, and then measured their performance against actual, realized data as it became available over the subsequent 1, 3, and 6-month periods. The table below summarizes the average Error and comparison of optimized ensemble models to the best-performing single-model baseline.
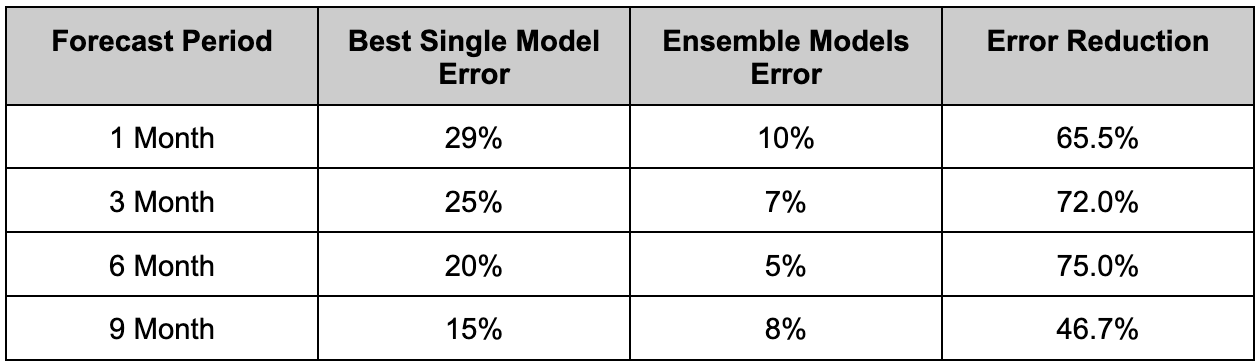
_Note: 80+ real world datasets were modeled. _
The empirical evidence demonstrates a dramatic and consistent reduction in forecast error across all time horizons. We observed two key findings:
- Significant Accuracy Gains: The ensemble approach yielded a substantial, two-thirds reduction in error for short-term (1-3 month) forecasts.
- Superior Long-Range Robustness: Most notably, the performance gap widened over a longer forecast horizon. The ensemble's 75% reduction in error for the 6-month forecast proves its superior ability to generalize and remain stable, mitigating the cumulative uncertainty that typically degrades single-model performance over time.
Conclusion
Lifesight Adaptive Forecasting Framework, a sophisticated ensemble approach moves beyond a single-model paradigm by synthesizing the strengths of diverse methodologies [1, 3], resulting in forecasts with demonstrably superior accuracy and robustness. For our marketing partners, this translates directly into quantifiable business value: more reliable strategic planning, optimized budget allocation, and a data-driven foundation for campaign management. This framework is not static; it is an evolving system. In our next technical brief, we will deconstruct the core components that drive its performance, including:
- Hyperparameter Optimization: Our methodology for fine-tuning models beyond standard defaults to achieve optimal performance for specific datasets.
- Advanced Ensemble Selection: The techniques we employ for dynamically weighting and selecting models, including methods for localized model application.
- Precision-Driven Loss Metrics: A look at why we move beyond standard error to utilize metrics like MAPE and CRPS to align our forecasts directly with business objectives.
References
[1] H. Wu and D. Levinson, "The ensemble approach to forecasting: A review and synthesis," Transportation Research Part C: Emerging Technologies, vol. 132, 2021, Art. no. 103357. [2] L. Du, R. Gao, P. N. Suganthan, and Z. Wang, "Bayesian Optimization Based Dynamic Ensemble for Time Series Forecasting," Information Sciences, vol. 591, 2022, doi: 10.1016/j.ins.2022.01.010. [3] I. D. Mienye and Y. Sun, "A Survey of Ensemble Learning: Concepts, Algorithms, Applications, and Prospects," IEEE Access, vol. 10, pp. 99182-99212, 2022, doi: 10.1109/ACCESS.2022.3207287. [4] R. Godahewa, K. Bandara, G. I. Webb, S. Smyl, and C. Bergmeir, "Ensembles of localised models for time series forecasting," Knowledge-Based Systems, vol. 233, 2021, Art. no. 107518. [5] S. J. Taylor and B. Letham, "Forecasting at scale," The American Statistician, vol. 72, no. 1, pp. 37-45, 2018, doi: 10.1080/00031305.2017.1380080. [6] O. Triebe, H. Hewamalage, P. Pilyugina, N. Laptev, C. Bergmeir, and R. Rajagopal, "NeuralProphet: Explainable Forecasting at Scale," 2021, [Online]. Available: arXiv:2111.15397 [cs.LG]. [7] F. R. Alharbi and D. Csala, "A Seasonal Autoregressive Integrated Moving Average with Exogenous Factors (SARIMAX) Forecasting Model-Based Time Series Approach," Inventions, vol. 7, no. 4, p. 94, Oct. 2022. [8] M. A. A. Mamun, M. S. Rahman, and M. R. Islam, "A Comparison of Machine Learning Models for Predicting Rainfall in Urban Metropolitan Cities," in 2023 26th International Conference on Computer and Information Technology (ICCIT), 2023, pp. 1-6. doi: 10.1109/ICCIT60451.2023.10441295. [9] A. Iqbal, M. D. R. Al-Mamun, Sk. Subbu, and M. S. Al-Muid, "A comparative study of machine learning algorithms for time series forecasting," in 2016 3rd International Conference on Electrical Engineering and Information Communication Technology (ICEEICT), 2016, pp. 1-6. doi: 10.1109/ICEEICT.2016.7873099. [10]https://wandb.ai/wandb_fc/articles/reports/What-Is-Bayesian-Hyperparameter-Optimization-With-Tutorial---Vmlldzo1NDQyNzcw [11] Winkler, Robert & Makridakis, Spyros. (1983). The Combination of Forecasts. Journal of the Royal Statistical Society. Series A (General). 146. 150-157. 10.2307/2982011.
Updated 3 months ago
