Ridge Regression
Robust inference with Regularized Ridge Regression
Ridge Regression in Marketing Mix Modeling
1. Introduction to Ridge Regression
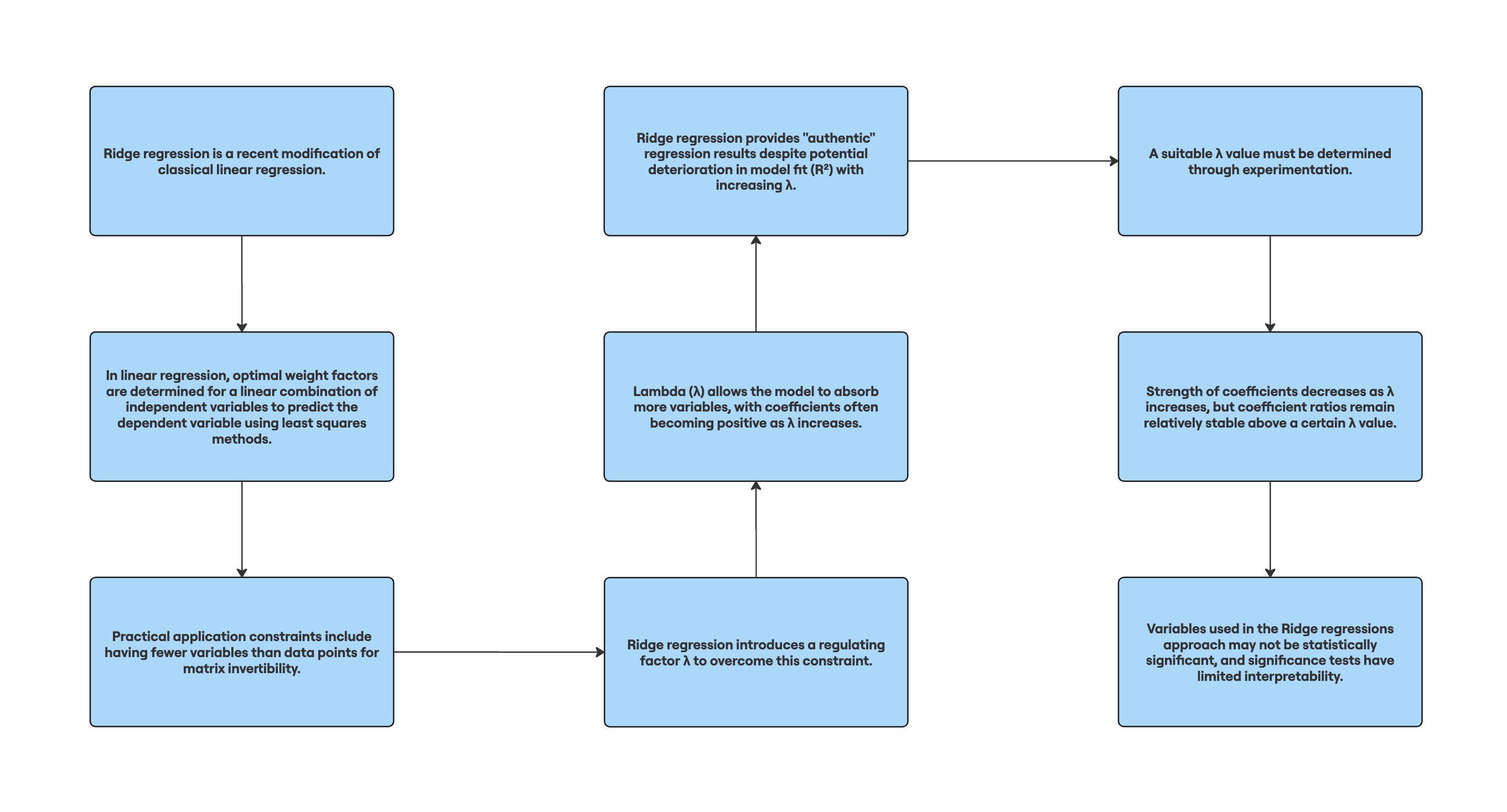
Ridge Regression is a powerful extension of classical linear regression, particularly valuable in Marketing Mix Modeling (MMM). It addresses issues of multicollinearity and overfitting, common challenges in marketing data analysis.
2. What is Ridge Regression?
The Basic Idea
Ridge Regression is a modification of linear regression that introduces a penalty term to the model. This penalty helps to constrain the size of the coefficients, making the model more stable and less prone to overfitting.
Simplifying the Concept
In MMM, we often deal with many related marketing variables. Ridge Regression helps us handle these interrelated variables by slightly adjusting their impacts, resulting in a more robust and reliable model.
3. Key Components of Ridge Regression
3.1 The Penalty Term (Lambda)
The core of Ridge Regression is the regularization parameter, lambda (λ). This parameter controls the strength of the penalty applied to the coefficients.
3.2 Coefficient Shrinkage
As λ increases, the coefficients of the model are "shrunk" towards zero, but not exactly to zero. This shrinkage helps in dealing with multicollinearity.
3.3 Bias-Variance Tradeoff
Ridge Regression introduces a small amount of bias to the model, but it can significantly reduce the variance, often leading to better overall predictions.
4. The Ridge Regression Formula
4.1 Classical Linear Regression
The standard linear regression aims to minimize:
min β Σ(yi - Xiβ)²4.2 Ridge Regression
Ridge Regression adds a penalty term:
min β [Σ(yi - Xiβ)² + λΣβj²]Where λ is the regularization parameter.
5. How Ridge Regression Works in MMM
5.1 Handling Multicollinearity
In MMM, variables like TV advertising and digital advertising might be correlated. Ridge Regression helps to stabilize the estimates of their individual effects.
5.2 Improved Predictive Power
By reducing overfitting, Ridge Regression often leads to models that generalize better to new data, crucial for forecasting in marketing.
5.3 Variable Selection
While Ridge Regression doesn't perform explicit variable selection, it can indicate the relative importance of different marketing channels by the magnitude of their shrunk coefficients.
6. Implementing Ridge Regression
6.1 Standardization
Before applying Ridge Regression, it's crucial to standardize the variables:
Xij_std = (Xij - mean(Xj)) / sd(Xj)6.2 Selecting Lambda
Cross-validation is commonly used to select an optimal λ value. This involves:
- Splitting the data into K folds
- Training models with different λ values
- Selecting the λ that minimizes cross-validated error
6.3 The Ridge Estimator
The Ridge estimator is given by:
β̂ridge = (X'X + λI)⁻¹X'y7. Comparative Analysis: OLS vs. Ridge Regression
Here's a hypothetical MMM scenario comparing Ordinary Least Squares (OLS) and Ridge Regression:
| Variable | OLS Coefficient | Ridge Coefficient (λ=0.1) | Ridge Coefficient (λ=1.0) |
|---|---|---|---|
| TV Advertising | 0.5 | 0.45 | 0.35 |
| Digital Ads | 0.3 | 0.28 | 0.22 |
| Print Media | 0.2 | 0.18 | 0.14 |
| Radio | 0.1 | 0.09 | 0.07 |
| Promotions | 0.4 | 0.36 | 0.28 |
| R² | 0.85 | 0.83 | 0.80 |
8. Advanced Concepts in Ridge Regression
8.1 Bayesian Interpretation
Ridge Regression can be interpreted as a Bayesian estimation with a prior distribution on β:
β ~ N(0, σ²/λ)8.2 Generalized Ridge Regression
For more flexibility, different penalty terms can be applied to different variables:
min β [Σ(yi - Xiβ)² + Σλjβj²]9. Why Ridge Regression is Important in MMM
Ridge Regression offers several benefits for Marketing Mix Modeling:
- Handles multicollinearity among marketing variables
- Improves model stability and predictive performance
- Provides more reliable estimates of marketing effects
- Allows inclusion of a larger number of variables
By using Ridge Regression, marketers can develop more comprehensive and robust models of marketing effectiveness, leading to more informed decision-making and optimized marketing strategies.
Updated 3 months ago
